One of my earlier series of work was based on the exploration of the Golden Ratio and the Fibonacci sequence. I created a number of two and three-dimensional works that depicted these separate but related concepts. One of the works, Hive depicts the relationship between the Golden Ratio, the Fibonacci sequence and the family tree of honeybees.

*Hive*, oil, encaustic wax, intaglio and relief prints on rice paper, bee hive material, all mounted on cradled wood panel, 16” x 16”

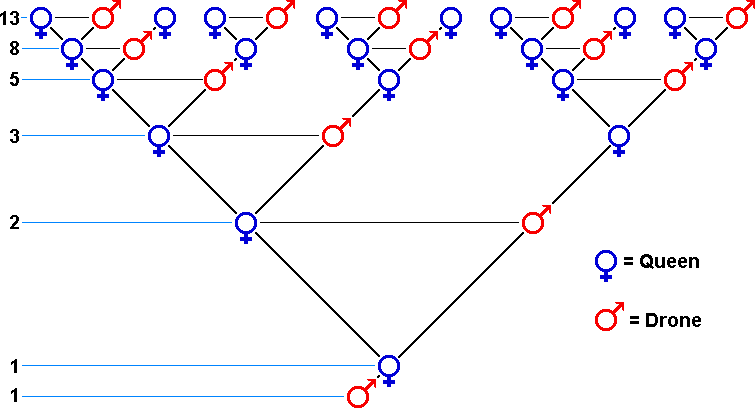
The Fibonacci sequence of numbers goes like this: 0 1 1 2 3 5 8 13 21 34 45 79… Each number is the sum of two preceding numbers. The growth of a honeybee family tree will follow the Fibonacci sequence because of its unique reproductive pattern. There is only one mother in the hive - the queen bee. A male bee (drone) is born from an unfertilized queen’s egg. The drone does not have a father. Female bees (worker bees) have two parents - a drone and the queen.

This table shows the ancestry of the drone and worker bees. Note the number sequences.

I find it easier to view this sequence graphically:

(source: http://www.dave-cushman.net/bee/fibonacci.html)

So, how is the Fibonacci sequence connected to the Golden Ratio? Well, as the sequence progresses, the ratio between each number approaches 1.618 (eg. 13 divided by 8 equals 1.625). This number is considered the Golden Ratio. Just to give you a bit more to chew on, the Fibonacci sequence and the Golden Ratio can be graphed:

(source: https://www2.nau.edu/lrm22/lessons/fibonacci/fibonacci.html)

Hive, 16 x 16 x 1.5 inches. Wood, encaustic wax, bee hive material, oil pigments, intaglio and relief prints on rice paper — *Hive*

Mathematical marvels